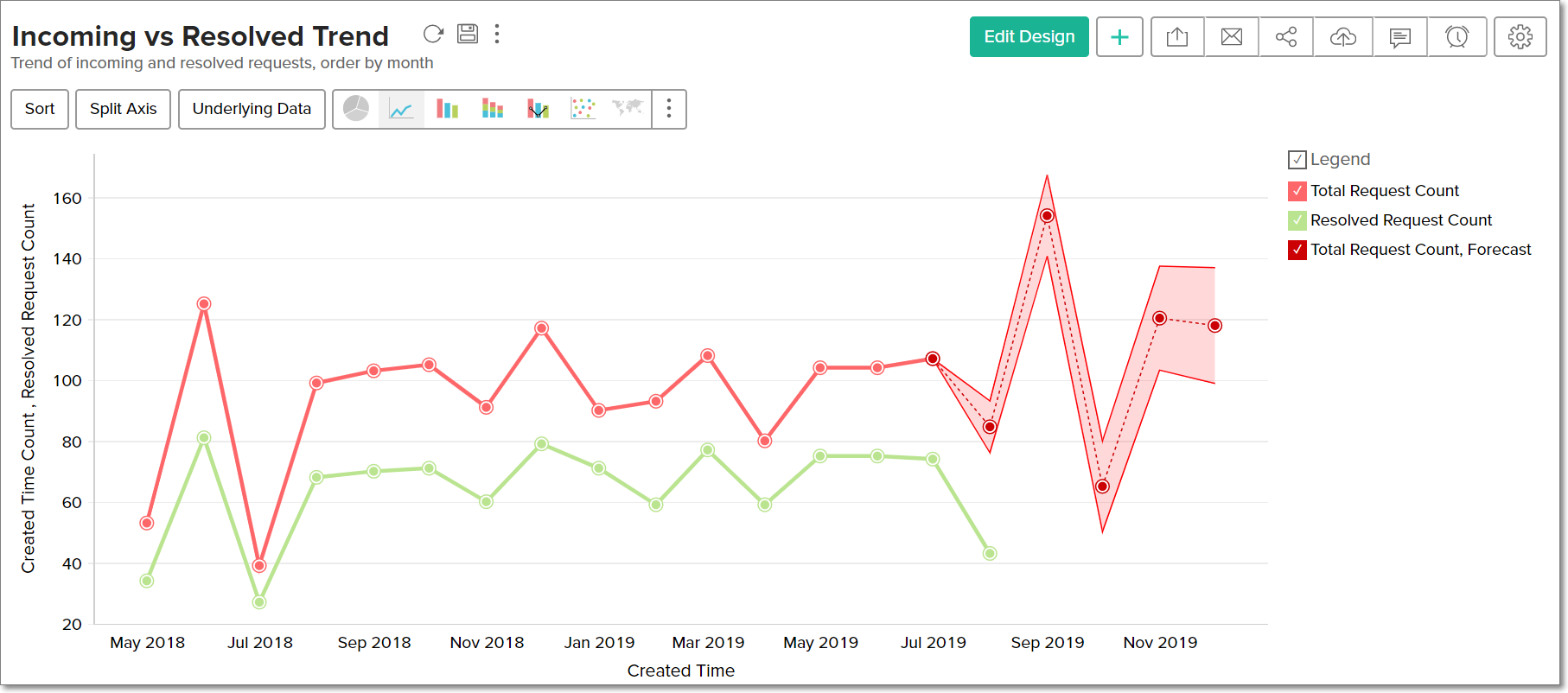
Analytics Plus での予測の仕組み

Analytics Plus は、さまざまな手法を使用してデータを分析し、パターンを識別し、将来の値を正確に予測する強力な予測エンジンを提供します。予測エンジンでは、予測モード、予測するユニット数、過去のデータで無視するデータポイントの数、予測データポイントに適用する書式設定の種類など、さまざまなカスタマイズが可能です。

サポートされているデータ系列
予測モデルの選択
選択した予測モデルの検証
予測データ

サポートされているデータ系列

Analytics Plus では、連続した時系列データ (等間隔で収集されたデータ) にプロットされた少なくとも 1 つの集計コラムを持つレポートに予測を適用できます。予測エンジンでは、データを正確に分析して予測するために、時系列内に少なくとも 6 つの連続したデータポイントが必要です。データポイントの数が増えると、データ予測の精度が向上します。

データに欠損値がある場合、Analytics Plus は最も頻度の低い間隔を使用して、欠損データポイントの値を自動的に入力します。値の 40% 以上が欠損している場合、予測は不可能になります。

注記：正確な予測を確実に行うには、予測値の数が利用可能なデータポイントの 40% を超えないようにしてください。つまり、データ系列で 10 個のデータポイントが利用可能な場合は、正確な結果を得るために最大 4 個のデータポイントを予測します。

予測モデルの選択

時系列データで識別されたパターンを活用して、予測エンジンは最初に予測モデルのセットを選択します。データに対して最適な結果を提供するモデルが、特定のデータ系列の予測モデルとして選択されます。

Analytics Plus で利用できる予測モデルは次のとおりです。これらの各モデルには複数のサブカテゴリがあります。

回帰
季節性トレンド Loess 分解（STL）
指数平滑化法（ETS）
自己回帰和分移動平均（ARIMA）

必要なモデルを選択することも、Analytics Plus にデータに最適な予測モデルを自動的に計算させることもできます。

回帰

回帰は、データ系列の動作を分析して、さまざまな値間の関係を識別します。パターンを確立すると、線形、対数、指数、べき乗、多項式（最大 7 次）などのさまざまな回帰モデルが計算されます。これらのモデルはそれぞれ出力をプロットし、R 二乗値 (または決定係数) を計算することで最終モデルが識別されます。最も高い R 二乗値を持つモデルが、データ系列に最適な回帰モデルとして選択されます。

季節性トレンド Loess 分解（STL）

このモデルは、トレンド、季節性、およびエラー (またはランダム性) のコンポーネントを利用して将来のデータポイントを計算します。データ系列内の 3 つのコンポーネントを識別すると、STL モデルは 2 つの方法のいずれかを使用して将来の値を計算します。

トレンド、季節性、ランダム性を特定する

データに最適な STL モデルを選択するには、時系列データ内のトレンド、季節性、ランダム性の存在を識別する必要があります。

トレンド：これは、時間の経過に伴う一連の均一な増加または減少を指します。予測エンジンは、回帰モデルを使用してトレンドの存在を検出します。回帰モデルを使用して描画された線が直線の場合、データ系列にはトレンドがありません。ただし、描画された線に傾斜がある場合は、データ系列にトレンドがあることを示します。
季節性：これは、データ系列内で一定の間隔で繰り返される一般的なパターンであり、スペクトル解析を使用して計算されます。
ランダム性: ランダム性またはエラーとは、データ系列内で特定されたパターンを持たないデータ系列内のランダムなポイントを指します。

3 つの要素に基づいて、加法モデルまたは乗法モデルのいずれかを使用して将来の値が計算されます。加法モデルではトレンド、季節性、ランダム性が加算され、乗法モデルでは 3 つの要素が乗算されます。

加法モデル: このモデルでは、時系列内の各コンポーネント（トレンド、季節性、エラー）の寄与はほぼ同じです。
乗法モデル: 乗法モデルでは、トレンドと季節性の要素が相互に乗算され、エラーコンポーネントに追加されます。

データ系列に最適な STL モデルは、二乗平均平方根誤差 (RMSE) 値を計算することによって特定されます。季節性トレンド Loess 分解モデルでは、ランダムポイントの平滑化も考慮されます。

指数平滑化法（ETS）

ETS モデルでは、予測値は過去の観測値の加重合計であり、過去の観測値の加重は指数的に減少します。したがって、データ系列の最近の値は、予測値に対してより大きな影響力を持ちます。したがって、指数平滑化法モデルは、将来のデータポイントを計算するために最近の値の方が重要である場合に最適です。

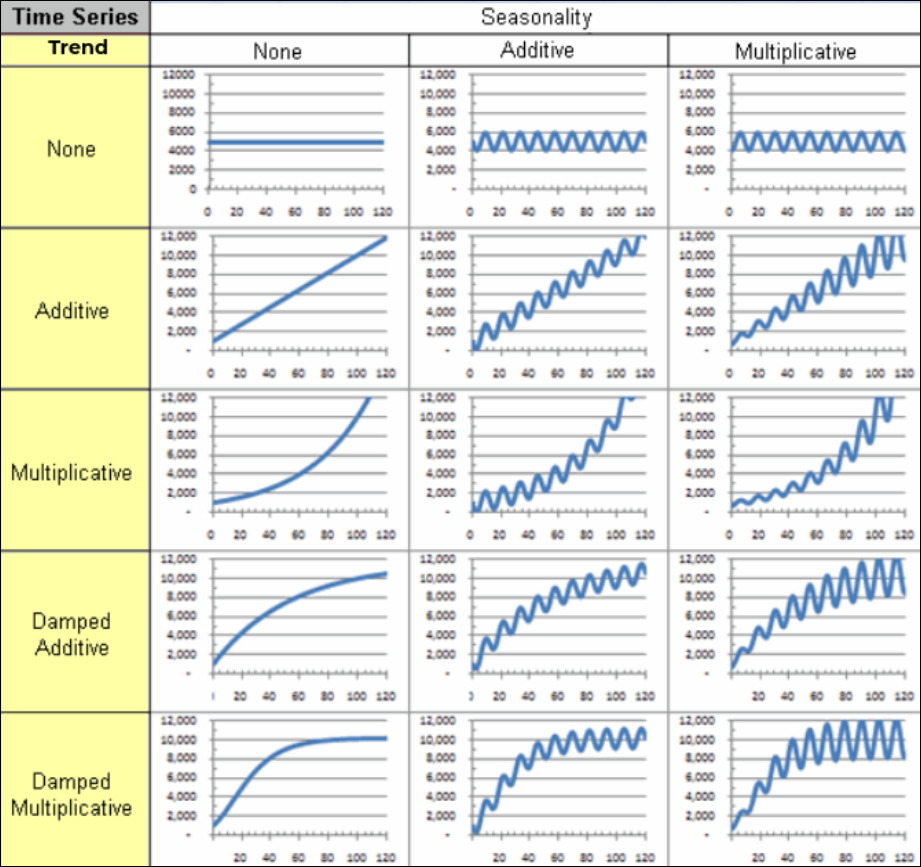
Analytics Plus の予測エンジンは、さまざまな種類の時系列データに対して、さまざまな指数平滑化法を提供します。次の図は、ETS モデルを生み出すさまざまなトレンドと季節性コンポーネントのさまざまな組み合わせを示しています。

ETS モデルを使用してデータを予測する際には、いくつかの平滑化パラメーターが必要です。これらのパラメーターは以下のとおりです。

アルファ：平滑化係数またはレベルの平滑化係数として知られるこのパラメーターは、過去の値の影響が指数関数的に減少する速度を制御します。この値は 0 から 1 までの範囲にする必要があります。
ベータ：これはトレンドの平滑化係数であり、トレンドコンポーネントの影響を制御します。この値は 0 から 1 までの範囲にする必要があります。
ガンマ：これは季節性の平滑化パラメーターであり、季節コンポーネントの影響を制御します。この値は 0 から 1 までの範囲にする必要があります。
ファイ：減衰係数として知られるこの係数は、減衰率を制御し、グラフを滑らかにするために使用されます。この値は 0 から 1 までの範囲にする必要があります。
頻度：これは、季節性が発生するまで、つまり季節パターンが繰り返されるまでに必要なデータポイントの合計数を示します。この値の範囲は 2 から、利用可能なデータポイント数の半分の上限までです。

必要な指数平滑化法モデルを選択することも、赤池情報量規準 (AIC) 法を使用してデータ系列に最適な ETS モデルを自動的に識別することもできます。

自己回帰和分移動平均（ARIMA）

これは、ホワイトノイズまたは基礎となるデータ生成プロセスの元の信号が抽出されるまで、連続的な変換に依存する時系列モデリングの従来のアプローチです。自己回帰プロセスと移動平均を採用して、起こりうるエラーとともに系列の性質を伝播します。ARIMA モデルは、適切なトレンドや季節性の要素のないランダムなデータ系列に最適です。

以下は、ARIMA モデルを使用してデータを予測する際に関係するさまざまなパラメーターです。

自己回帰順序（p）：このパラメーターは、データ系列内の自己回帰項の数を示します。
移動平均順序（q）：このパラメーターは、時系列内の各瞬間に考慮される以前のエラー値の数を示します。
統合順序（d）：これは、定常信号（つまり、時間の経過に伴って平均が一定である信号）を生成するためにデータポイントを微分する必要がある回数を表します。
頻度：このパラメーターは、スペクトル解析を使用して生成された季節性プロファイルを示し、反復的な影響を除去するために使用されます。

選択した予測モデルの検証

予測エンジンは、さまざまなモデルの結果を比較し、赤池情報量規準 (AIC) を使用してグラフを予測するのに最適なモデルを特定します。この計算の最後に 2 つのモデルが同様の結果を提供する場合は、ベイズ情報規準 (BIC) 法を使用して、データ系列に最適な最終予測モデルを選択します。

予測データ

これらの計算に基づいて、Analytics Plus は最も適した予測モデルを使用し、データ系列の将来のデータポイントを生成します。