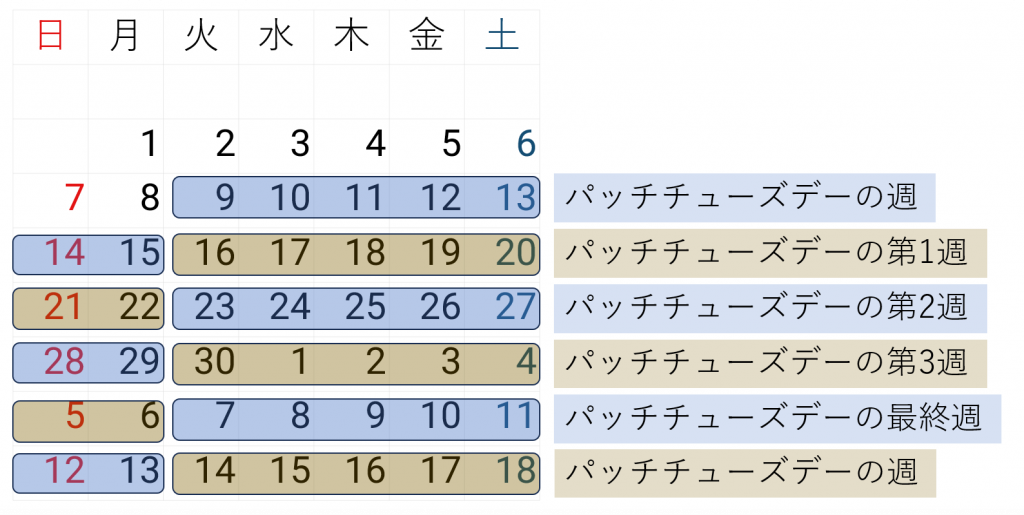
パッチチューズデー準拠における週の数え方
質問1
配布ポリシーの「配布スケジュール」において「基準」に「パッチチューズデー準拠」を選択した場合、「配布を行う週/曜日」における週の選択に応じて具体的にはどのような期間が指定されるのでしょうか。
回答1
「パッチチューズデー準拠」では、火曜日から次の月曜日までを1つの週として扱います。
「配布を行う週/曜日」で設定できる週は、以下のとおりです。
- パッチチューズデーの週(Patch Tuesday Week)
パッチチューズデーである毎月第2火曜日から開始し、その6日後の月曜日までで終了する7日間です。 - パッチチューズデーの第1週(First week after Patch Tuesday)
「パッチチューズデーの週」の次の週を表します。すなわち、毎月第3火曜日から開始し、その6日後の月曜日までで終了する7日間です。 - パッチチューズデーの第2週(Second week after Patch Tuesday)
「パッチチューズデーの週」の次の次の週を表します。すなわち、毎月第4火曜日から開始し、その6日後の月曜日までで終了する7日間です。 - パッチチューズデーの第3週(Third week after Patch Tuesday)
「パッチチューズデーの週」の3週間後の週を表します。上記「パッチチューズデーの第2週」の次の週です。 - パッチチューズデーの最終週(Last week before next patch tuesday)
次回のパッチチューズデーの直前の7日間を表します。すなわち、毎月第1火曜日から開始し、第2火曜日の前日の月曜日までで終了する7日間です。
質問2
「パッチチューズデーの第3週」と「パッチチューズデーの最終週」は同一の週を表す場合があるようですが、どのような場合に両者は同じ週となるのでしょうか。
回答2
一般に、火曜日は(他の曜日も同様ですが)1つの月の中に4回のみ存在する場合と5回存在する場合があります。
火曜日が4回のみ存在する月においては、その月の第4火曜日の7日後が、翌月の第1火曜日となります。
火曜日が5回存在する月においては、その月の第5火曜日の7日後が、翌月の第1火曜日となります。
よって、
「火曜日が4回のみ存在する月の第2火曜日から、その翌月の第2火曜日の前日まで」という期間の中においては、「パッチチューズデーの第2週」( = 第4火曜日から始まる7日間)の次の週が、「パッチチューズデーの最終週」である。
「火曜日が5回存在する月の第2火曜日から、その翌月の第2火曜日の前日まで」という期間の中においては、「パッチチューズデーの第3週」の次の週が「パッチチューズデーの最終週」である。
と言えます。
また、上記「回答1」で述べたように、「パッチチューズデーの第3週」は「パッチチューズデーの第2週」の次の週です。
ゆえに、本件質問への回答として、
「火曜日が4回のみ存在する月の第2火曜日から、その翌月の第2火曜日の前日まで」という期間の中においては、【「パッチチューズデーの第2週」の次の週は「パッチチューズデーの第3週」である】ということと【「パッチチューズデーの第2週」の次の週は「パッチチューズデーの最終週」である】ということが同時に成立するため、「パッチチューズデーの第3週」と「パッチチューズデーの最終週」は同じ週である。
「火曜日が5回存在する月の第2火曜日から、その翌月の第2火曜日の前日まで」という期間の中においては、「パッチチューズデーの第2週」の次の週は「パッチチューズデーの第3週」であり、かつ、「パッチチューズデーの第3週」の次の週は「パッチチューズデーの最終週」である。
ということが成り立ちます。
ある月の第1火曜日の日にちが、その月の日数から28を引いた数よりも大きいとき、その月には火曜日は4回のみ存在します。したがって、ある月のパッチチューズデー(第2火曜日)の日にちが、その月の日数から21を引いた数よりも大きいとき、その月には火曜日は4回のみ存在します。パッチチューズデーの日にちが、その月の日数から21を引いた数以下であるとき、その月には火曜日は5回存在します。